Style Transfer

Neural Style Transfer

Before carrying out a style transfer process, let’s make it clear that in fact this is.

Style transfer is a process of modifying the style of an image and at the same time preserving its content. The article that defines this whole process can be seen at https://arxiv.org/pdf/1508.06576.pdf.

A simple example can be seen in the figure below. (ref: https://www.techleer.com/articles/466-insight-into-fast-style-transfer-in-tensorflow/)

Equations: https://arxiv.org/pdf/1508.06576.pdf

In this way, the idea is simple. There is an input image and a style image. The output will be your stylized input image. That is:

• Input + Style -> Stylized input

Let’s program a neural network, step by step, to do the style transfer. Let’s start by importing some libraries.

Imposing libraries

import numpy as np
from PIL import Image
import tensorflow as tf
from keras import backend as K
from keras.models import Model
from keras.applications.vgg16 import VGG16

from scipy.optimize import fmin_l_bfgs_b

Defining some parameters

media_rgb_imagenet = [123.68, 116.779, 103.939] # Average RGB values of ImageNet images
peso_conteudo = 0.02
peso_estilo = 4.5
variacao_peso = 0.995
variacao_fator_custo = 1.25
largura_imagem = 260
altura_imagem = 260
canais = 3 # R G B

#Reading input image and placing in the chosen standard size (260x260)
img_entrada = Image.open('Imagens/win_xp.jpg')
img_entrada = img_entrada.resize((altura_imagem,largura_imagem))
img_entrada.save('entrada.png')
img_entrada

# Lendo imagem de estilo e colocando no tamanho padrão escolhido (500x500)
img_estilo = Image.open('Imagens/barnes.jpg')
img_estilo = img_estilo.resize((altura_imagem,largura_imagem))
img_estilo.save('estilo.png')
img_estilo

Normalization by the mean and transformation from RGB to BGR

img_entrada_arr = np.asarray(img_entrada, dtype="float32") # shape = (largura_imagem, altura_imagem, canais)
img_entrada_arr = np.expand_dims(img_entrada_arr, axis=0) # shape = (1, largura_imagem, altura_imagem, canais)
img_entrada_arr[:, :, :, 0] -= media_rgb_imagenet[2]
img_entrada_arr[:, :, :, 1] -= media_rgb_imagenet[1]
img_entrada_arr[:, :, :, 2] -= media_rgb_imagenet[0]
img_entrada_arr = img_entrada_arr[:, :, :, ::-1] # Troca RGB por BGR

img_estilo_arr = np.asarray(img_estilo, dtype="float32") # shape = (largura_imagem, altura_imagem, canais)
img_estilo_arr = np.expand_dims(img_estilo_arr, axis=0) # shape = (1, largura_imagem, altura_imagem, canais)
img_estilo_arr[:, :, :, 0] -= media_rgb_imagenet[2]
img_estilo_arr[:, :, :, 1] -= media_rgb_imagenet[1]
img_estilo_arr[:, :, :, 2] -= media_rgb_imagenet[0]
img_estilo_arr = img_estilo_arr[:, :, :, ::-1] # Troca RGB por BGR

Neural Network Model

We will use a pre-trained Convolutional Neural Network (CNN) model, the VGG-16. This model is the right choice for image processing. In addition, it allows us to separately extract the content and style of an image, and that is exactly what we want. Then, we will pass the two images through the VGG and initialize the image to be generated in a random image.

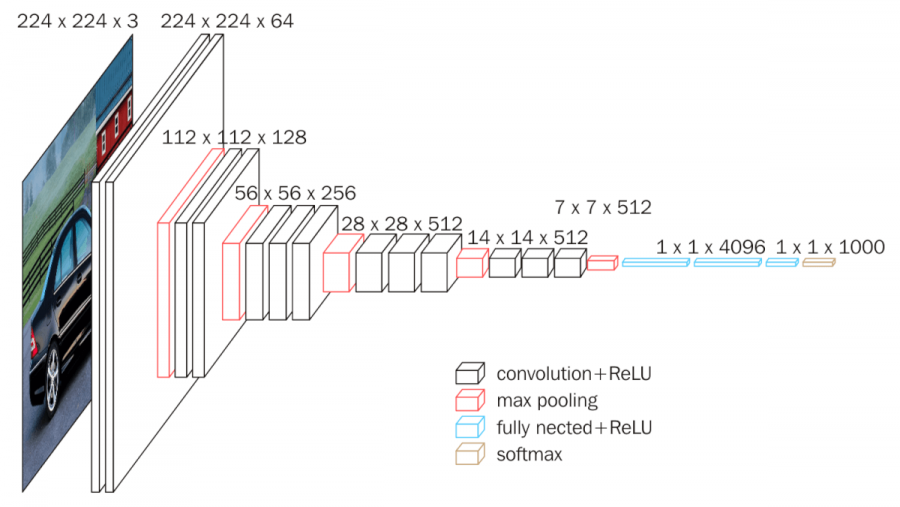
Keep in mind that we will not use fully-connected layers (blue) and softmax (yellow). They act like a classifier that we do not need here. Let’s use only feature pullers, ie convolutional layers (black) and MaxPooling (red). In this model, the information is important and, using MaxPooling on CNN, we are throwing out a large number of pixel values from the previous layer and we are keeping only the highest values.

entrada = K.variable(img_entrada_arr)
estilo = K.variable(img_estilo_arr)
imagem_combinada = K.placeholder((1, largura_imagem, altura_imagem, canais))

tensor_entrada = K.concatenate([entrada, estilo, imagem_combinada], axis=0)
model = VGG16(input_tensor=tensor_entrada, include_top=False, weights='imagenet')

model.summary()

_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
input_1 (InputLayer)         (None, None, None, 3)     0         
_________________________________________________________________
block1_conv1 (Conv2D)        (None, None, None, 64)    1792      
_________________________________________________________________
block1_conv2 (Conv2D)        (None, None, None, 64)    36928     
_________________________________________________________________
block1_pool (MaxPooling2D)   (None, None, None, 64)    0         
_________________________________________________________________
block2_conv1 (Conv2D)        (None, None, None, 128)   73856     
_________________________________________________________________
block2_conv2 (Conv2D)        (None, None, None, 128)   147584    
_________________________________________________________________
block2_pool (MaxPooling2D)   (None, None, None, 128)   0         
_________________________________________________________________
block3_conv1 (Conv2D)        (None, None, None, 256)   295168    
_________________________________________________________________
block3_conv2 (Conv2D)        (None, None, None, 256)   590080    
_________________________________________________________________
block3_conv3 (Conv2D)        (None, None, None, 256)   590080    
_________________________________________________________________
block3_pool (MaxPooling2D)   (None, None, None, 256)   0         
_________________________________________________________________
block4_conv1 (Conv2D)        (None, None, None, 512)   1180160   
_________________________________________________________________
block4_conv2 (Conv2D)        (None, None, None, 512)   2359808   
_________________________________________________________________
block4_conv3 (Conv2D)        (None, None, None, 512)   2359808   
_________________________________________________________________
block4_pool (MaxPooling2D)   (None, None, None, 512)   0         
_________________________________________________________________
block5_conv1 (Conv2D)        (None, None, None, 512)   2359808   
_________________________________________________________________
block5_conv2 (Conv2D)        (None, None, None, 512)   2359808   
_________________________________________________________________
block5_conv3 (Conv2D)        (None, None, None, 512)   2359808   
_________________________________________________________________
block5_pool (MaxPooling2D)   (None, None, None, 512)   0         
=================================================================
Total params: 14,714,688
Trainable params: 14,714,688
Non-trainable params: 0
_________________________________________________________________

The problem to be solved

The problem to be solved for style transfer is an optimization problem. To do this, we must minimize three functions:

• Cost of content (distance between input and output images);
• Style cost (distance between style and output images);
• Cost of total variation (regularization - spatial smoothness to minimize the output image).

Cost of content

def custo_conteudo(conteudo, combinacao):
    return K.sum(K.square(combinacao - conteudo))

layers = dict([(layer.name, layer.output) for layer in model.layers])

camada_conteudo = 'block2_conv2' #Usando a camada após a primeiro convolução os resultados são melhores
camada_caracteristicas = layers[camada_conteudo]
camada_conteudo_caracteristicas = camada_caracteristicas[0, :, :, :]
caracteristicas_combinacao = camada_caracteristicas[2, :, :, :]

custo = K.variable(0.)
custo += peso_conteudo * custo_conteudo(camada_conteudo_caracteristicas, caracteristicas_combinacao)

Style Cost

For the calculation of the cost of style, it is necessary to calculate the Gram matrix:

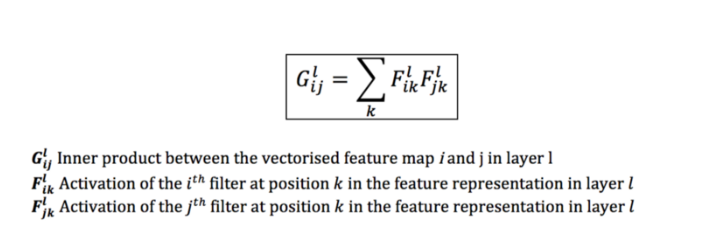
And then, the definition of the style cost:

def gram_matrix(x):
    caracteristicas = K.batch_flatten(K.permute_dimensions(x, (2, 0, 1)))
    gram = K.dot(caracteristicas, K.transpose(caracteristicas))
    return gram

def calc_custo_estilo(estilo, combincacao):
    estilo = gram_matrix(estilo)
    combincacao = gram_matrix(combincacao)
    tamanho = largura_imagem * altura_imagem
    return K.sum(K.square(estilo - combincacao)) / (4. * (canais ** 2) * (tamanho ** 2))

camadas_estilo = ["block1_conv2", "block2_conv2", "block3_conv3", "block4_conv3", "block5_conv3"]
for nome in camadas_estilo:
    caracteristicas_camada = layers[nome]
    caracteristicas_estilo = caracteristicas_camada[1, :, :, :]
    caracteristicas_combinacao = caracteristicas_camada[2, :, :, :]
    custo_estilo = calc_custo_estilo(caracteristicas_estilo, caracteristicas_combinacao)
    custo += (peso_estilo / len(camadas_estilo)) * custo_estilo

Total variation cost

This cost function serves as smoothing to smooth the gradients in the training and to prevent the increase of noise.

def custo_variacao_total(x):
    a = K.square(x[:, :largura_imagem-1, :altura_imagem-1, :] - x[:, 1:, :altura_imagem-1, :])
    b = K.square(x[:, :largura_imagem-1, :altura_imagem-1, :] - x[:, :altura_imagem-1, 1:, :])
    return K.sum(K.pow(a + b, variacao_fator_custo))

custo += variacao_peso * custo_variacao_total(imagem_combinada)

Optimization

Now that we have our cost functions defined, we can define our style transfer process as an optimization problem where we minimize our overall loss (which is a combination of loss of content, style and total variation).

In each iteration, we will create an output image so that the distance (difference) between output and input / style in the corresponding resource layers is minimized.

saidas = [custo]
saidas += K.gradients(custo, imagem_combinada)

def calculo_custo_e_gradientes(x):
    x = x.reshape((1, largura_imagem, altura_imagem, canais))
    outs = K.function([imagem_combinada], saidas)([x])
    custo = outs[0]
    gradients = outs[1].flatten().astype("float64")
    return custo, gradients

class Evaluator:

    def custo(self, x):
        custo, gradientes = calculo_custo_e_gradientes(x)
        self._gradientes = gradientes
        return custo

    def gradientes(self, x):
        return self._gradientes

evaluator = Evaluator()

Optimizer

In style transfer learning, we will use a deterministic l-bfgs optimizer instead of the descent gradient or Adam. But why this?

Unlike a classifier, in this case, the optimizer does not receive several different samples and attempts to generalize all of them. In style transfer, the optimizer receives the same image several times. Also, l-bfgs determines the optimal direction and distance to be traveled by doing a line search. In stochastic problems like classifications and regressions is an expensive approach computationally, however it is a good approach to transfer style. In this way, l-bfgs learns faster than Adam in the problem in question.

x = np.random.uniform(0, 255, (1, largura_imagem, altura_imagem, canais)) - 128. #irandom initiation
n = 10 # numero de iteracoes
for i in range(n):
    x, custo, info = fmin_l_bfgs_b(evaluator.custo, x.flatten(), fprime=evaluator.gradientes, maxfun=20)
    print("Iteracao %d completa com custo: %d" % (i + 1, custo))

x = x.reshape((largura_imagem, altura_imagem, canais))
x = x[:, :, ::-1] # BGR para RGB
# Retira a normalização pela média da ImageNet
x[:, :, 0] += media_rgb_imagenet[2]
x[:, :, 1] += media_rgb_imagenet[1]
x[:, :, 2] += media_rgb_imagenet[0]

x = np.clip(x, 0, 255).astype("uint8") # mantem os valores entre 0 e 255
output_image = Image.fromarray(x)
output_image.save('output.png')
output_image

Viewing images

combinada = Image.new("RGB", (largura_imagem*3, altura_imagem))
x_offset = 0
for image in map(Image.open, ['entrada.png', 'estilo.png', 'output.png']):
    combinada.paste(image, (x_offset, 0))
    x_offset += largura_imagem
combinada.save('vis.png')
combinada